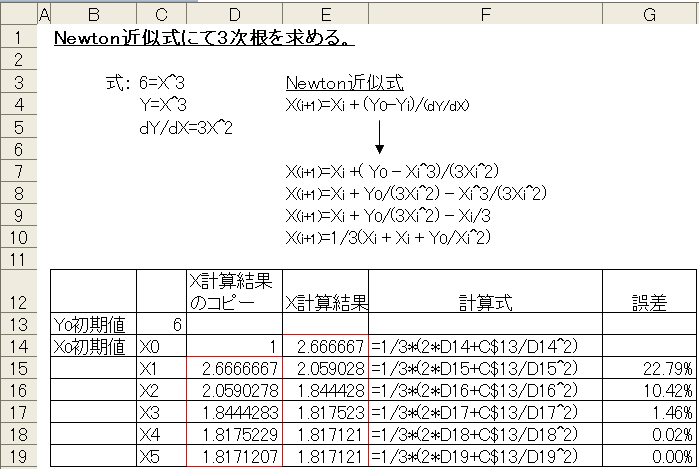
下の画面は3次根を求めています。
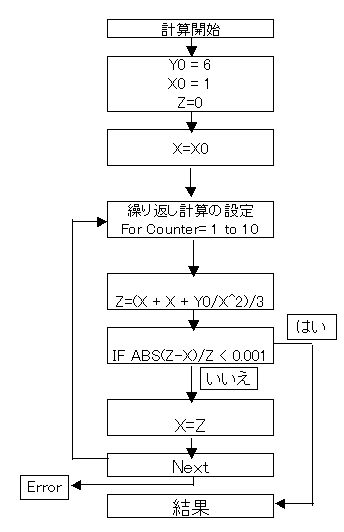
ニュートン近似で計算を繰り返すと、正解に近付く基本原理を以下説明します。
下画面を参照してください。
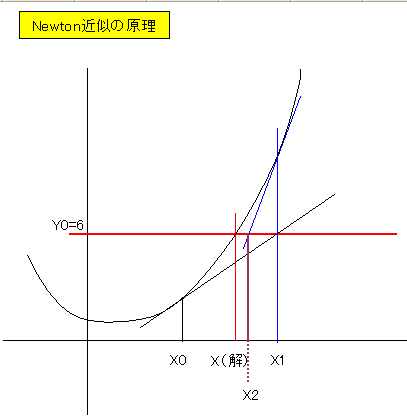
多次元曲線のYが6の時のX(解)を求めます。(赤線)
1.初期値X0で多次元曲線の接線を求めます。その直線とY=6直線との交点X1を2番目の解とします。
次に、次の図を見てください。
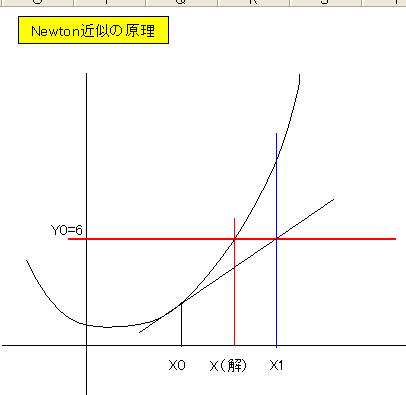
この図を見て判るように、X2はX(解)により近づいています。
これを繰り返すと、より正解に近付き、前回計算値との誤差も小さくなり、正解とします。
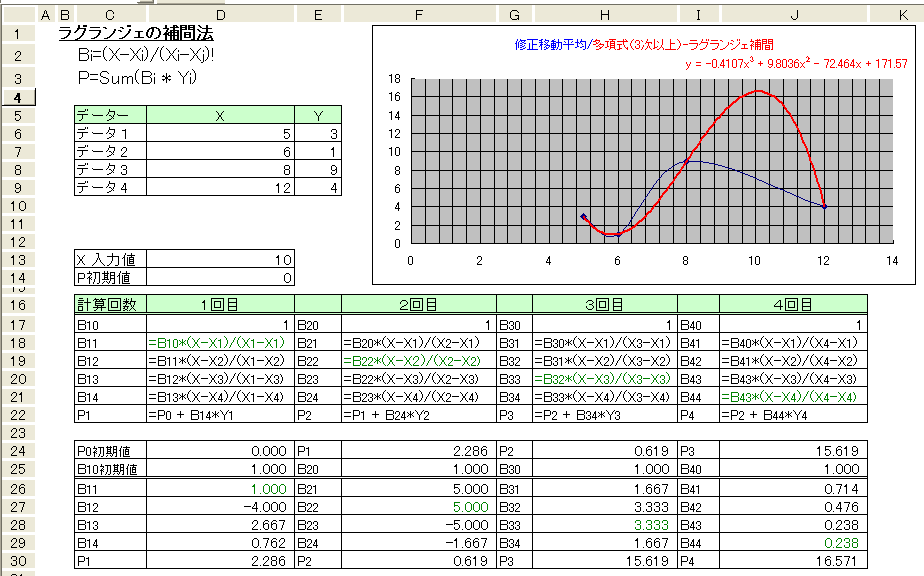
有名なのがラグランジェ補間法です。
次の例は、少し極端なデータにしています。
X入力値が10とし、ラグランジェ補間法で、Yを求めた結果は16.57です。
グラフで示す赤色曲線は多項式近似曲線(ラグランジェと同じ)です。青色は修正移動平均の曲線です。
修正移動平均の方が良さそうに見えますが、どちらが正しいとは言い切れません。
解析をする傾向を考慮して、いずれの方法が妥当か決めればよいと思います。